Physics of the Pole Vault Physics of the Pole Vault
by Kimo Morris I am not an expert in physics. Fortunately, the general concepts of pole vault physics are rather simple. Here, I present a VERY simple model with which to have fun. As an example of how any average vaulter can figure out their maximum potential height, we can do some simple math to get a ball park figure. The basic idea is this - a pole vaulter takes his/her horizontal acceleration and converts it into vertical acceleration (counteracting the acceleration of gravity) through the use of a compressible spring (that would be the pole). To derive an equation, one must first make a few assumptions to start. Okay, so you may recall that FORCE equals MASS times ACCELERATION (good ole' Newton's f=ma equation). In the case of the vault, this means that the amount of force applied to the pole at the plant equals the mass of the vaulter (his/her weight) times the vaulter's acceleration at the plant (where acceleration is the measure of change in the velocity or speed). So the first assumption we will make is that the "energy" at the bottom of the plant is converted to vertical lift without any loss. This of course does not happen in real life. No vaulter can convert 100% of the energy created at the plant into vertical lift. Much of it is lost in pole vibration, dissipation in the fiberglass, technique, etc. However, by making this assumption, we can make a mathematical model to figure out what the absolute highest height would be for a vaulter with a given weight and speed. So, we will start our model by saying that 100% of the KINETIC ENERGY gets converted to POTENTIAL ENERGY. From your intro to physics book, you know that the equation for calculating potential energy as one increases their height off the ground is: PE = mgx where m is mass (calculated from weight), g is the acceleration of gravity, and x is the height off the ground. Again, from your physics book, you can also get the equation for calculation Kinetic Energy: KE = 1/2 mv2 where m is mass, and v is velocity (which is the same as speed in our equation). Since we've made the assumption that all the kinetic energy will equal the potential energy, you can just make the equations equal to each other like this: mgx = 1/2 mv2 If you solve for x (height), you get x = (1/2 v2)/g This solution says a lot! First, notice that mass no longer appears in the equation. In fact, there are only two things left in the equation - speed and gravity. Obviously, gravity is constant. Thus, your absolute height will be determined by how fast you run! Now, let's come back down to reality. There is a lot more to pole vaulting than just running fast. One must work on proper technique throughout the entirety of the vault. The better your technique, the less energy you will lose throughout the vault. But, a generality can be made here. Assuming it were possible for two vaulters to have the exact same technical skills, the one that jumps the highest is the one that can run the fastest. So, let's get back to our equation. Suppose you can run a 100m race in 12 seconds. Your speed (velocity) would therefore be 100m/12s = 8.33 m/s. Gravity is 9.8 m/s2. Plugging this into the equation and you get: x = (1/2 v2)/g = (1/2 (8.33m/s)2)/9.8m/s2 = 3.54m which is the same as 11'8" But wait a minute! That does not seem that high. Remember, this is just a mathematical model. Our little equation does not know the difference between a ball of lead and a water balloon, let alone the shape of a human body. It simply calculates a distance based on the center of mass of an object. From a math standpoint, our pole vaulter is just a little sphere with a center of mass in the middle. The fact is, the center of mass of a normal human adult is around 3' 6" off the ground. So, our estimate of height means that your center of mass at the end of the vault will be 11' 8" above the center of mass when you are still on the ground. Thus, you must add 3' 6" and 11' 8" to get 15' 2". At this point, again, we must bring reality back into it. By getting completely inverted and pushing off the top of the pole, a vaulter can actually "pull" and then "push" their center of mass higher as the pole uncoils (unbends). See my UCI picture from 1994 to get a visual idea of this. Really good vaulters can push their hips (center of mass) up as much as 4' beyond their top hand grip. Clearly, there is much more to the vault. Other important variables
come into play. To truly understand the vault from an advanced
perspective, one must understand how the vault is affected by
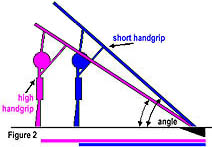
things like the TAKE OFF ANGLE. The height of ones hand grip will also effect the angle at take off. If we have two vaulters of identical height, but one vaulter holds higher (closer to the top end of the pole), then the vaulter who holds higher will create a smaller angle at take off (Figure 2). This means that as you improve and you begin to hold higher on the pole, you will have to compensate by running faster, keeping your center of mass high, and producing more force at the plant. Along with the angle of take off, the distance of ones take off from the box also affects the vault. Since the distance of take off is related to the angle of take off, it is hard to see why they are separate things. However, think of it this way. The further away from the box you are, the greater the distance that you must carry your energy to complete the vault. Again, the shorter you are, or the higher you hold, the greater your take off distance will be from the box. Speed at the plant is key for this variable. Let's face it, holding higher means you have to run faster and hit the back of the box harder!
Vaulting poles themselves have undergone much evolution since the late 1960s. We now use fiberglass, or fiberglass-carbon composite poles. Thus, poles have the capacity to bend and act just like a spring. Poles are built with a variety of resistances depending on the amount of fiberglass in the pole, and thus each pole can withstand a certain amount of force applied to them depending on their rating. If you are a vaulter, this is not new to you. You are aware that all poles have a "weight" ascribed to them. However, from a physics stand point, this assigned weight is more or less arbitrary. Remember: we are concerned with FORCE, which is a function of MASS and ACCELERATION. However, pole vault manufacturers do not put a force rating on a pole because normal human beings don't think in terms of force. Rather, we think about the two variables that result in force, namely how much you weigh (mass) and how fast you run (without getting too technical, your speed, or velocity, is factored in to get acceleration which is the change in velocity over time). Since the variation in the speed of vaulters is less than the variation in the weight of vaulters, it is reasonable that poles are rated by weight. You should therefore pay close attention to the weight marked on a pole. You should use that mark as a starting point to figure out what pole to start with. But since you are all physics wizzes, you all know that speed is an equally important variable. Assuming your weight does not change much, then as you run faster and faster, you will continue to produce a greater force at the plant, imparting a greater load on the pole. The solution is then to use a pole with a greater weight rating. The result, since your weight does not change in flight, is that you will be whipped off the top of the pole with a greater force. Think about it in terms of a spring. The stronger the spring, the more force is required to load it, but at the same time, that stronger spring will throw a light object with greater force, provided that the lighter object (that would be you, the vaulter) is capable of loading the stiffer spring. Thus, as you get better, you will actually start using poles that are rated higher than your weight. For comparison, when I was in the prime of my vaulting career, I weighed 124 lbs, but the pole I used was rated at 155lbs, 31lbs over my weight! The only way I could achieve this was to produce the same amount of force at the plant as an average 155lb vaulter would on the same pole. Remember f = ma? I achieved this by running faster. To learn more about the mechanics of the vault, I have listed a few websites below that will help. Please send me feedback and let me know if this page was useful to you. Happy vaulting! - Kimo Return to Kimo's Pole Vault Page |
||||||
|
Back to Kimo's Home Page | Graduate Research | Personal Bio | Kauai Scuba | Email Kimo Morris |
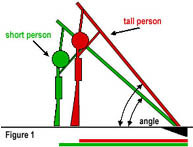 This is roughly determined by the angle the pole makes with the
ground at the plant when your right arm (for right-handed vaulters)
is straight above your head. If two vaulters hold in the exact
same place on a pole, but one vaulter is taller, then the taller
vaulter will create a larger angle at takeoff, and will subsequently
be closer to the box (Figure 1). The shorter vaulter will have to compensate by either running
faster, or modifying their takeoff to give the effect of having
the same angle at takeoff of the taller vaulter. This is why coaches
constantly tell their vaulters to take shorter, quicker strides
at the end of the run, so the center of mass is as high as possible
at the take off. Another technique used by more advanced vaulters
is "jumping into" the vault, that is, beginning the long-jump-style
take off before the bottom of the pole has contacted the box.
What advanced vaulters do to accomplish this is to jump outside
of their standard take off, also known as the plumb line (plumb
line is defined as the place where your take off toe touches the
runway when you are standing perfectly straight with the pole
in the box and your arms extended above your head without leaning
backward or forward - we all do this when we check our step).
This is known as "taking off outside". I DO NOT recommend doing
this unless you are experienced. If you do not have enough speed
at the plant, taking off outside could lead to serious problems.
Only attempt taking off outside under the instruction of an experienced
coach.
This is roughly determined by the angle the pole makes with the
ground at the plant when your right arm (for right-handed vaulters)
is straight above your head. If two vaulters hold in the exact
same place on a pole, but one vaulter is taller, then the taller
vaulter will create a larger angle at takeoff, and will subsequently
be closer to the box (Figure 1). The shorter vaulter will have to compensate by either running
faster, or modifying their takeoff to give the effect of having
the same angle at takeoff of the taller vaulter. This is why coaches
constantly tell their vaulters to take shorter, quicker strides
at the end of the run, so the center of mass is as high as possible
at the take off. Another technique used by more advanced vaulters
is "jumping into" the vault, that is, beginning the long-jump-style
take off before the bottom of the pole has contacted the box.
What advanced vaulters do to accomplish this is to jump outside
of their standard take off, also known as the plumb line (plumb
line is defined as the place where your take off toe touches the
runway when you are standing perfectly straight with the pole
in the box and your arms extended above your head without leaning
backward or forward - we all do this when we check our step).
This is known as "taking off outside". I DO NOT recommend doing
this unless you are experienced. If you do not have enough speed
at the plant, taking off outside could lead to serious problems.
Only attempt taking off outside under the instruction of an experienced
coach.